VAE：变分推断、MC估计和重要性采样

本文将从表征学习的角度以及隐变量模型的角度探讨VAE模型，重点讲述VAE的三个技术

隐变量的意义

高斯混合模型

VAE从概率密度估计的角度来说是一种mixture model

基本的高斯混合模型写做：

\(p(x) = \sum_{i=1}^{k} w_i \mathcal{N}(x | \mu_i, \Sigma_i)\)

其中的i是指第i个高斯分布，\(u_i\)和\(\Sigma_i\)​指的是第i个高斯分布的均值和方差

但是高斯混合模型的拟合能力是有限的，假如我们用一簇无穷多的高斯分布来拟合最终的分布, 那这个拟合能力不久非常好了吗？怎么去建模这个无穷多(infinite)的分布呢?

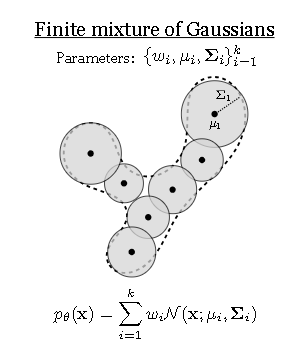
这图摘自S9868 Deep learning课程，非常形象的展示了混合模型做了什么：用高斯分布把数据流形填满

怎么做无限混合呢？VAE给出的解答是把累加变成了积分

\(p_{\theta}(x) = \int_{z} \mathcal{N}(x; g_{\theta}(z), \Sigma_{\theta}(z)) \mathcal{N}(z; 0, I) dz\)

也即是假设混合高斯的权重符合一个分布，属于隐变量\(z\)，并且我们的高斯分布是隐变量参数化的结果,即式中的条件分布,分别参数化了高斯分布的均值\(g_{\theta}\)和方差\(\Sigma_{\theta}(z))\)

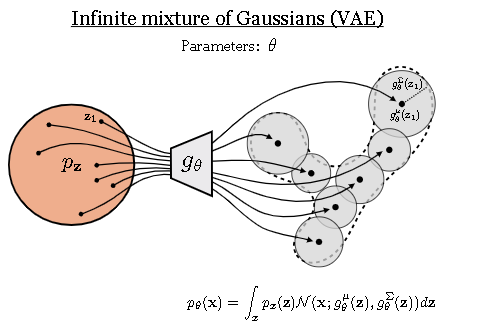
S9868 也给出了无限混合的感性可视化，参数化帮助我们的mixture model更加的flexible了，能自己学习怎么去填满这个数据流形。

这里的\(P(z)\)和\(P_\theta(x|z)\)​都假设的高斯分布，当然我们也能make an infinite mixture of the autoregressive distribution and so on. ,从这个角度来说mixture分布是meta model 可以用其他的密度估计模型替代

这个概率摸底建模是一个积分的无穷项，这里我们需要用到统计学的一个基本技术，用MC采样来估计这个积分

\(p_{\theta}(x) = \int p_{\theta}(x|z)p_z(z)dz = \mathbb{E}_{z \sim p_z(z)}[p_{\theta}(x|z)] \approx \frac{1}{M} \sum_{i=1}^{M} p_{\theta}(x|z^{(i)}), \quad z^{(i)} \sim p_z\)

MC采样的直观理解是求平均值的这个过程本身就蕴含了采样过程

当我们概率建模有了，接下来就是计算极大似然来优化参数！

\(E_{x \sim p_{data} }log P_{\theta}(x)\)​

极大似然认为最优的分布参数是一个定值，因此我们把数据扔进去优化一个maximal的似然值

\(\theta^* = \underset{\theta}{\arg\min} \frac{1}{M} \sum_{i=1}^{N} \log \left( \sum_{j=1}^{M} \mathcal{N}\left(x^{(i)}; g_{\theta}^{\mu}\left(z^{(j)}\right), g_{\theta}^{\Sigma}\left(z^{(j)}\right)\right) \right)\)

以上都是在拟合概率，但是对于神经网络而言我们有的标签不是概率这太抽象了，我们只有从Pdata中获得的样本,如何优化这个混合模型？

把方差固定，优化这个似然值就变成优化\(||x-g_{\theta}^{\mu}||\),训练的步骤是我们采样一堆隐变量z，扔进网络\(g_{\theta}\)中产生一堆高斯分布的均值，然后在和一个batch的样本\(x\)​ 计算L2norm，这就是我们要的似然值.

重要性采样

我们在建模概率的时候是利用的MC采样来估计积分

\(p_{\theta}(x) \approx \frac{1}{M} \left( p_{\theta}(x|z^{(1)}) + p_{\theta}(x|z^{(2)}) + p_{\theta}(x|z^{(3)}) + \ldots \right)\)

遇到一个问题，往往高维空间MC采样的效率很低，往往会变成这样：

\(p_{\theta}(x) \approx \frac{1}{M} \left( 0 + p_{\theta}(x|z^{(2)}) + 0 + \ldots \right)\)​

这意味着要想精确的估计概率，必须要大量的采样，采样效率很低

这里引出本文的第二个技术，重要性采样：

\(p_{\theta}(x) = \mathbb{E}_{z \sim p_z}[p_{\theta}(x|z)] = \int p_z(z)p_{\theta}(x|z)dz = \int \frac{p_z(z)}{q_z(z)} p_{\theta}(x|z)q_z(z)dz = \mathbb{E}_{z \sim q_z}\left[\frac{p_z(z)}{q_z(z)} p_{\theta}(x|z)\right]\)

重要性采样给出一种不用在原始分布p中采样，而在新的分布q中采样，这是一种减少方差的采样技术

最优的\(q(z)\)正比于\(p(z)P_{\theta}(x|z)\) 后者正比于\(P(x,z)\) 它又正比于\(p_{\theta}(z|x)\)，所以可以证明最优的\(q(z)\)等于\(p_{\theta}(z|x)\)

\(p_{\theta}(x) \approx \frac{1}{M} \sum_{j=1}^{M} \frac{p_z(z^{(j)})}{p_{\theta}(z^{(j)}|x)} p_{\theta}(x|z^{(j)})\), \(z^{(j)} \sim p_{\theta}(Z|x)\)

最开始的

在重要性采样的语境下，\(p_{\theta}(z|x)\) 这个z就是和建模\(p_{\theta}(x)\)最相关的z

变分推断

高斯混合模型的有点是隐变量分布是高斯分布，重要性采样的效率更高但是这里又出现了一个难以采样的分布\(P_{\theta}(z|x)\)​​ 这个时候引入最后一个重要的技巧，变分推断(Variational inference)

顺便吐槽一句，很多的教程都从变分推断出发，丝毫不讨论生成的过程，这和我生成模型又有什么关系呢 :D