Posted 2024-06-25Updated 2024-06-2516 minutes read (About 2358 words)0 visits

能量模型是分类器

本片要讲的是论文《Your Diffusion Model is Secretly a Zero-Shot Classifier》

首先这篇文章让我想起来之前看过的一篇论文，用能量模型来做分类器，能量模型把数据分布建模成能量：$p(\mathbf{x}) = \frac{e^{-E(\mathbf{x})}}{Z}$

其中概率和能量成反比，概率越高，能量越低

能量模型建模的两个主要难点就是配分函数如何求解或者近似，以及如何从分布中采样

能量模型建模联合概率的方式是同时输入x和y，成对的xy能量小，不成对的xy能量大例如，如果是普通判别网络做mnist分类：

$y = f_w(x)$
x:784维向量
y:10维向量
w神经网络f的参数

能量模型做分类：

$E = f_w(x,y)$
输入794维向量

能量模型如何构建？

$\text{假设数据集为} (x, y) \in (\mathbb{R}^D, \mathbb{R}), y \in {0, 1, 2, \ldots, K-1},\ \text{能量函数由神经网络参数化}
E(x, y; \theta) = -NN_{\theta}(x, y)[y], \text{这里的}[y]\text{表示不同的标签}。$

如何对$p(x,y)$进行建模？

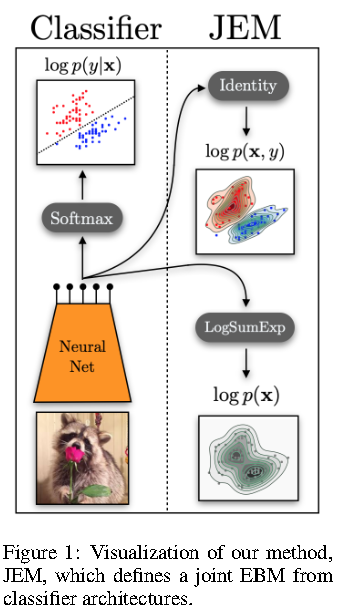
$\begin{align*}
\ln p_{\theta}(x, y) &= \ln p_{\theta}(y | x) + \ln p_{\theta}(x) \
&= \ln \left( \frac{\exp{NN_{\theta}(x)[y]}}{\sum_{y} \exp{NN_{\theta}(x)[y]}} \right) + \ln \left( \frac{\sum_{y} \exp{NN_{\theta}(x)[y]}}{Z_{\theta}} \right) \
&= \ln \text{softmax} {NN_{\theta}(x)[y]} + { \text{LogSumExp}{y} {NN{\theta}(x)[y]} - \ln Z_{\theta} }
\end{align*}$

可以看到同时建模分类和生成

对这个似然求导又会遇到老朋友，从$p_{\theta}(x)$中采样，这时候我们再一次利用朗之万动力学这个依靠数据梯度的梯度下降方法（SGLD），具体算法如下：

Classifier-free diffusion guidance

classifier guidence

得分函数的一个良好性质是使得我们不用去考虑归一化分母：

$\nabla_x \log \tilde{p}(x) = \nabla_x \log (p(x) \cdot Z) = \nabla_x (\log p(x) + \log Z) = \nabla_x \log p(x),$

利用贝叶斯公式，我们将条件生成拆解生一个生成器和一个分类器

$p(x \mid y) = \frac{p(y \mid x) \cdot p(x)}{p(y)} \
\implies \log p(x \mid y) = \log p(y \mid x) + \log p(x) - \log p(y) \
\implies \nabla_x \log p(x \mid y) = \nabla_x \log p(y \mid x) + \nabla_x \log p(x),$

$p(y∣x)$ 正是分类器和其他判别模型试图拟合的内容：xxx 是某个高维输入，而 y 是目标标签。如果我们有一个可微分的判别模型来估计 $p(y∣x)$，那么我们也可以轻松获得 $\nabla_x \log p(y|x)$。将无条件扩散模型转换为条件模型所需要的只是一个分类器,Sohl-Dickstein 等人和 Song 等人提到，扩散模型可以通过这种方式事后进行条件化，但 Dhariwal 和 Nichol 真正强调了这一点，并展示了分类器引导如何通过增强条件信号显著提高样本质量，即使在与传统条件建模结合使用时也是如此。为此，他们将条件项按一个因子进行缩放：

$\nabla_x \log p_{\gamma}(x|y) = \nabla_x \log p(x) + \gamma \nabla_x \log p(y|x)$

其中，$\gamma$被称为引导尺度，将其调高到超过 1 的效果是放大条件信号的影响。

事实上这意味着我们将分布的条件部分提升到一个幂次，这对应于调整该分布的温度：γ\gammaγ 是一个逆温度参数。如果 γ>1\gamma > 1γ>1，这会通过将概率质量从最不可能的值转移到最可能的值来使分布变得更加尖锐并聚焦于其模式（即温度降低）。分类器引导允许我们仅对捕捉条件信号影响的分布部分应用这种温度调节。

在语言建模中，现在很常见的是先训练一个强大的无条件语言模型，然后根据需要将其适应下游任务（通过少样本学习或微调）。表面上看，分类器引导使得图像生成能够实现同样的效果：可以先训练一个强大的无条件模型，然后在测试时根据需要使用一个单独的分类器对其进行条件化。

不幸的是，有一些问题使得这种方法不切实际。最重要的是，因为扩散模型是通过逐步去噪输入来操作的，任何用于引导的分类器也需要能够应对高噪声水平，以便在整个采样过程中提供有用的信号。这通常需要专门训练一个用于引导的分类器，在这种情况下，可能更容易端到端地训练一个传统的条件生成模型（或至少微调一个无条件模型以合并条件信号）。

但即使我们有一个噪声鲁棒的分类器，分类器引导在其效果上也是有限的，分类器经常会学习到一些不鲁棒的相关性（即使是那些经过训练对高斯噪声具有鲁棒性的分类器），结果是它们相对于输入的梯度可能指向不理想的方向。。

$p_{\gamma}(x \mid y) \propto p(x) \cdot p(y \mid x)^{\gamma}.$

classifier free

不需要训练一个单独的分类器。相反，我们训练一个条件扩散模型 p(x∣y)p(x \mid y)p(x∣y)，并引入条件丢失（conditioning dropout）：有一定比例的时间，条件信息 yyy 被移除（10-20% 的比例通常效果较好）。在实践中，通常用一个特殊的输入值来表示条件信息的缺失。由此得到的模型现在可以在提供条件信号时作为条件模型 p(x∣y)p(x \mid y)p(x∣y) 运行，也可以在没有条件信号时作为无条件模型 p(x)p(x)p(x) 运行。你可能会认为这会以条件建模性能为代价，但实际上这种影响似乎可以忽略不计。

这对我们有什么帮助呢？回想之前的贝叶斯定理，但让我们反过来应用

$p(y \mid x) = \frac{p(x \mid y) \cdot p(y)}{p(x)} \
\implies \log p(y \mid x) = \log p(x \mid y) + \log p(y) - \log p(x) \
\implies \nabla_x \log p(y \mid x) = \nabla_x \log p(x \mid y) - \nabla_x \log p(x).\nabla_x \log p_{\gamma}(x \mid y) = \nabla_x \log p(x) + \gamma (\nabla_x \log p(x \mid y) - \nabla_x \log p(x)) \
\nabla_x \log p_{\gamma}(x \mid y) = (1 - \gamma) \nabla_x \log p(x) + \gamma \nabla_x \log p(x \mid y).$

为什么这比分类器引导效果好得多？主要原因是我们从生成模型构建了“分类器”。标准分类器可以取巧，忽略大部分输入 xxx 而仍然获得有竞争力的分类结果，而生成模型则没有这种奢侈。这使得生成的梯度更加鲁棒。另外，我们只需训练一个（生成）模型，并且条件丢失（conditioning dropout）很容易实现。

值得注意的是，从分类器无引导（classifier-free guidance）理念的发表到 OpenAI 的 GLIDE 模型的问世，时间窗口非常短，而 GLIDE 模型利用这一理念取得了巨大的效果，以至于有时这个理念被归功于后者！简单而强大的理念往往会迅速被采纳。在功效与简洁性的比例方面，分类器无引导与 dropout 相当，在我看来，真的是一个改变游戏规则的创新！

（事实上，GLIDE 论文中提到，他们最初训练了一个文本条件模型，并仅在微调阶段应用了条件丢失。或许这样做有充分的理由，但我怀疑这只是因为他们决定将这个理念应用于他们之前已经训练好的模型上！）

显然，引导代表了一种权衡：它显著提高了对条件信号的遵从性以及整体样本质量，但代价是多样性的巨大损失。在条件生成建模中，这通常是一个可以接受的权衡，因为条件信号往往已经捕捉了我们实际关心的大部分变异性，如果我们需要多样性，我们也可以简单地修改我们提供的条件信号。

后面关于这方面会出两篇代码上的讲解